下面是“勾股定理”一课的课堂教学：? 第一个环节：探索勾股定理的教学? 师(出示4幅图形和表格)：观察、计算各图中正方形A，B，C的面积，完成表格，你有什么发现?? 生：从表中可以看出A、B两个...

下面是“勾股定理”一课的课堂教学：?
第一个环节：探索勾股定理的教学?
师(出示4幅图形和表格)：观察、计算各图中正方形A，B，C的面积，完成表格，你有什么发现??



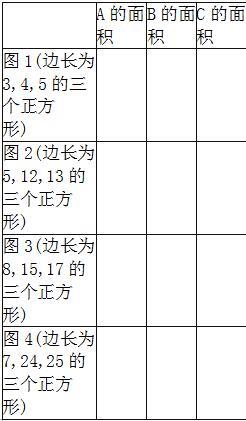
生：从表中可以看出A、B两个正方形的面积之和等于正方形C的面积。并且，从图中可以看出正方形A、B的边就是直角三角形的两条直角边，正方形C的边就是直角三角形的斜边，根据上面的结果，可以得出结论：直角三角形的两条直角边的平方和等于斜边的平方。?
第二个环节：证明勾股定理的教学?
教师给各小组分发制作好的直角三角形和正方形纸片，先分组拼图探究，在交流、展示，让学生在实践探究活动中形成新的能力(试图发现拼图和证明的规律：同一个图形面积用不同的方法表示)。?
学生展示略?
第三个环节：运用勾股定理的教学?
师(出示图形)：图形是由两个正方形组成的图形，能否剪拼为一个面积不变的新的正方形，若能，看谁剪的次数最少。?
生：可以剪拼成一个面积不变的新的正方形，设原来的两个正方形的边长分别是a，b，那么它们的面积和就是a2+b2，由于面积不变，所以新正方形的面积应该是a2+b2，所以只要是能剪出两个以a，b为直角边的直角三角形，把它们重新拼成一个边长为a2+b2的正方形就行了。?
第四个环节：挖掘勾股定理文化价值?
师：勾股定理揭示了直角三角形三边之间的数量关系，数与形密切联系起来。它在培养学生数学计算、数学猜想、数学推断、数学论证和运用数学思想方法解决实际问题中都具有独特的作用。勾股定理最早记载于公元前十一世纪我国古代的《周髀算经》，在我国古籍《九章算术》中提出“出入相补”原理证明勾股定理。在西方勾股定理又被成为“毕达哥拉斯定理”，是欧式几何的核心定理之一，是平面几何的重要基础，关于勾股定理的证明，吸引了古今中外众多数学家、物理学家、艺术家，甚至美国总统也投入到勾股定理的证明中来。它的发现、证明和应用都蕴涵着丰富的数学人文内涵，希望同学们课后查阅相关资料，了解数学发展的历史和数学家的故事，感受数学的价值和数学精神，欣赏数学的美。?
问题：?
(1)教学环节一的设计，你有怎样的启发；?
(2)教师引导学生利用图形证明勾股定理的过程，你是否认可?请给出你的看法和依据；?
(3)针对教学环节三、四的设计是否恰当?说说你的看法。